The MixColumns step executes matrix-vector multiplication column by column as per Galois Field 2 to power of 8. Although we won't describe this step in detail, it is important to note that this multiplication has the property of operating independently over each of the columns of the initial matrix, i.e. the first column when multiplied by the matrix, produces the first column of the resultant matrix. Watch the video for practical demonstration using logism.
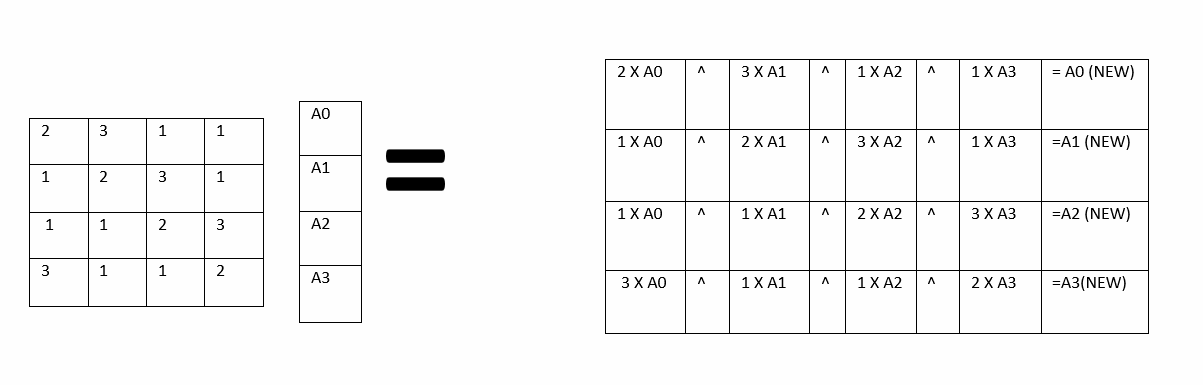
As you can see we should addition and multiplication in bit level, and in multiplication we specifically do multiply 2 and 3. Then how we can do these operation? We can think of addition as XOR operation on bit level, multiplying 2 as left shifting in bit level and multiplying 3? Combination of one left shift and one XOR operation. After multiplication we do finish mix columns step. One thing to keep in mind is that mix columns step is not executed in last round. watch the video below for a practical demonstration.
`timescale 1 ns/1 ps module MixColumns # ( parameter DATA_W = 128 //data width ) ( input clk, //system clock input reset, //asynch active low reset input valid_in, //input valid signal input [DATA_W-1:0] data_in, //input data output reg valid_out, //output valid signal output reg [DATA_W-1:0] data_out //output data ) ; wire [7:0] State [0:15]; //array of wires to form state array wire [7:0] State_Mulx2 [0:15]; //array of wires to perform multiplication by 02 wire [7:0] State_Mulx3 [0:15]; //array of wires to perform multiplication by 03 genvar i ; generate for(i=0;i<=15;i=i+1) begin :MUL assign State[i]= data_in[(((15-i)*8)+7):((15-i)*8)]; // filling state array as each row represents one byte ex: state[0] means first byte and so on assign State_Mulx2[i]= (State[i][7])?((State[i]<<1) ^ 8'h1b):(State[i]<<1); //Multiplication by {02} in finite field is done shifting 1 bit lift //and xoring with 1b if the most bit =1 assign State_Mulx3[i]= (State_Mulx2[i])^State[i]; // Multiply by {03} in finite field can be done as multiplication by {02 xor 01} end endgenerate always@(posedge clk or negedge reset) if(!reset)begin valid_out <= 1'b0; data_out <= 'b0; end else begin if(valid_in) begin //mul by 2 and mul by 3 are used to perform matrix multiplication for each column data_out[(15*8)+7:(15*8)]<= State_Mulx2[0] ^ State_Mulx3[1] ^ State[2] ^ State[3]; //first column data_out[(14*8)+7:(14*8)]<= State[0] ^ State_Mulx2[1] ^ State_Mulx3[2] ^ State[3]; data_out[(13*8)+7:(13*8)]<= State[0] ^ State[1] ^ State_Mulx2[2] ^ State_Mulx3[3]; data_out[(12*8)+7:(12*8)]<= State_Mulx3[0] ^ State[1] ^ State[2] ^ State_Mulx2[3]; /*********************************************************************************/ data_out[(11*8)+7:(11*8)]<= State_Mulx2[4] ^ State_Mulx3[5] ^ State[6] ^ State[7]; //second column data_out[(10*8)+7:(10*8)]<= State[4] ^ State_Mulx2[5] ^ State_Mulx3[6] ^ State[7]; data_out[(9*8)+7:(9*8)] <= State[4] ^ State[5] ^ State_Mulx2[6] ^ State_Mulx3[7]; data_out[(8*8)+7:(8*8)]<= State_Mulx3[4] ^ State[5] ^ State[6] ^ State_Mulx2[7]; /**********************************************************************************/ data_out[(7*8)+7:(7*8)]<= State_Mulx2[8] ^ State_Mulx3[9] ^ State[10] ^ State[11]; //third column data_out[(6*8)+7:(6*8)]<= State[8] ^ State_Mulx2[9] ^ State_Mulx3[10] ^ State[11]; data_out[(5*8)+7:(5*8)]<= State[8] ^ State[9] ^ State_Mulx2[10] ^ State_Mulx3[11]; data_out[(4*8)+7:(4*8)]<= State_Mulx3[8] ^ State[9] ^ State[10] ^ State_Mulx2[11]; /***********************************************************************************/ data_out[(3*8)+7:(3*8)]<= State_Mulx2[12] ^ State_Mulx3[13] ^ State[14] ^ State[15]; //fourth column data_out[(2*8)+7:(2*8)]<= State[12] ^ State_Mulx2[13] ^ State_Mulx3[14] ^ State[15]; data_out[(1*8)+7:(1*8)]<= State[12] ^ State[13] ^ State_Mulx2[14] ^ State_Mulx3[15]; data_out[(0*8)+7:(0*8)]<= State_Mulx3[12] ^ State[13] ^ State[14] ^ State_Mulx2[15]; end valid_out <= valid_in; end endmodule